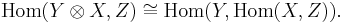Tensor-hom adjunction

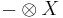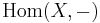In mathematics, the tensor-hom adjunction is that the functors $- \otimes X$ and $\operatorname{Hom}(X,-)$ form an adjoint pair:

$\operatorname{Hom}(Y \otimes X, Z) \cong \operatorname{Hom}(Y,\operatorname{Hom}(X,Z)).$

This is made more precise below. The order "tensor-hom adjunction" is because tensor is the left adjoint, while hom is the right adjoint.

General Statement

Say R and S are (possibly noncommutative) rings, and consider the right module categories C = Mod-R and D = Mod-S. Fix a bimodule A=_RA_S. The functor 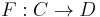$F:C\to D$ taking X_R to the tensor product 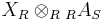$X_R\otimes_R{}_RA_S$ is left adjoint to the functor 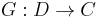$G:D\to C$ taking Y_S to Hom_S(_RA_S, Y_S).

An analogous statement holds for left modules.

References

Bourbaki, Nicolas (1989), Elements of mathematics, Algebra I, Springer-Verlag, ISBN 3-540-64243-9